指数函数

以下为《指数函数》的无排版文字预览，完整格式请下载

下载前请仔细阅读文字预览以及下方图片预览。图片预览是什么样的，下载的文档就是什么样的。

2.1.2

指数函数及其性质

引入

问题1、某种细胞分裂时，由1个分裂成

2个，2个分裂成4个，1个这样的细胞分

裂x次后，得到的细胞个数y与x的函数

关系式是什么？

问题

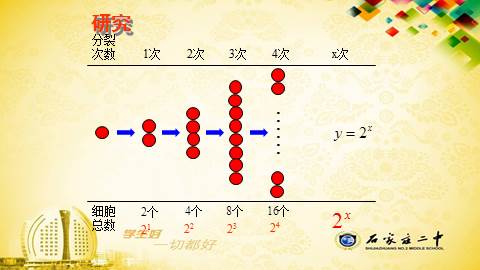
21

22

23

24

研究

引入

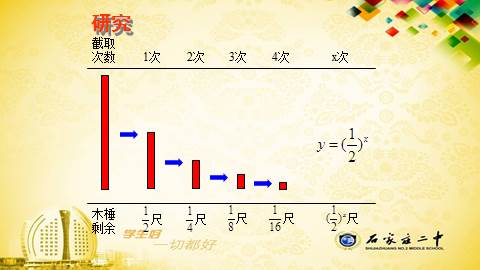
问题2、《庄子XXXXX天下篇》中写道：“一尺

之棰，日取其半，万世不竭。”请你写出

截取x次后，木棰剩余量y关于x的函数关

系式？

问题

研究

提炼

指数函数的定义:

一般地，函数 叫做指数函数，其中 x 是自变量, 函数的定义域是 R.

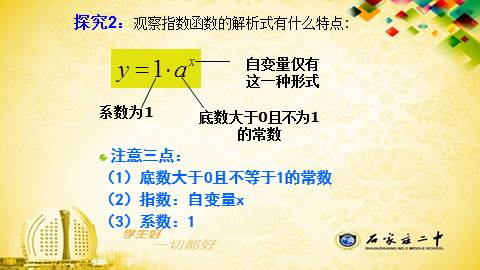
探究2：观察指数函数的解析式有什么特点:

注意三点：

（1）底数大于0且不等于1的常数

（2）指数：自变量x

（3）系数：1

当a=1时,

当a=0时，

当a<0时，

x≤0

x>0

当a>0时,

对任意实数有意义

为了便于研究，规定：a>0 且a≠1

（口答）判断下列函数是不是指 数函数，为什么？

√

√

例题

③ ( )

①

②

④

⑤

⑥

⑦

⑧

√

二、指数函数的图象和性质：

设问1：我们研究函数的性质，通常通过函数图象

来研究函数的哪几个性质？

1.定义域 2.值域 3.单调性 4.奇偶性

5.最值 6.对称性等

设问2：那么得到函数的图象一般用什么方法？

列表、求对应的x和y值、描点、作图

8

7

6

5

4

3

2

1

-6

-4

-2

2

4

6

8

7

6

5

4

3

2

1

-6

-4

-2

2

4

6

8

7

6

5

4

3

2

1

-6

-4

-2

2

4

6

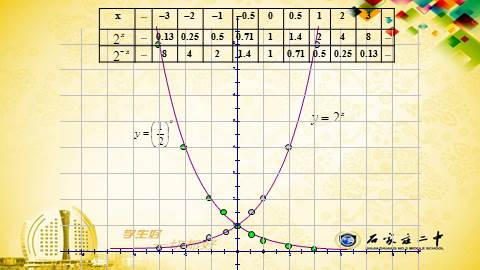
（1）函数

（2）两个函数图象有什么共同点？

（3）两个函数的图象有何不同之处？

的图象与函数

什么关系？

有

思考：

问题1：这两个函数图像关于y轴对称，

问题2：这两个函数图像都过定点（0.1）

问题3： 的函数图像 随着自变量x的增大函数值y也在增大，则指数函数 在R上为增函数；

而 的图像随自变量x的增大而函数值y在减小，所以指数函数 在R上位减函数。

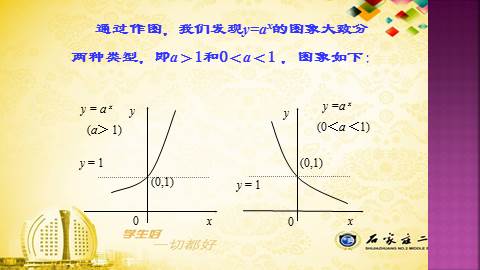
通过作图，我们发现y=ax的图象大致分

两种类型，即a＞1和0＜a＜1 ，图象如下：

图 象

性 质

y

x

0

y=1

(0,1)

y=ax

(a>1)

y

x

(0,1)

y=1

0

y=ax

(0<a<1)

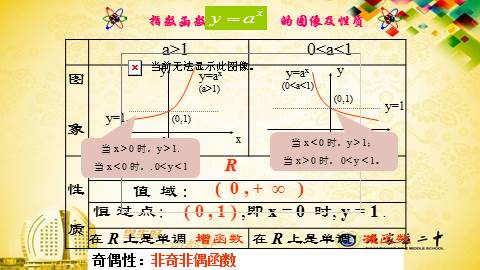
定 义 域 :

值 域 :

恒 过 点：

在 R 上是单调

在 R 上是单调

a>1

0<a<1

R

( 0 , + ∞ )

( 0 , 1 ) ,即 x = 0 时, y = 1 .

增函数

减函数

指数函数 的图像及性质

当 x > 0 时，y > 1.

当 x < 0 时，. 0< y < 1

当 x < 0 时，y > 1；

当 x > 0 时， 0< y < 1。

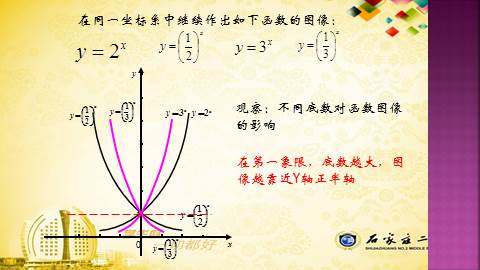
在第一象限，底数越大，图像越靠近Y轴正半轴

观察：不同底数对函数图像的影响

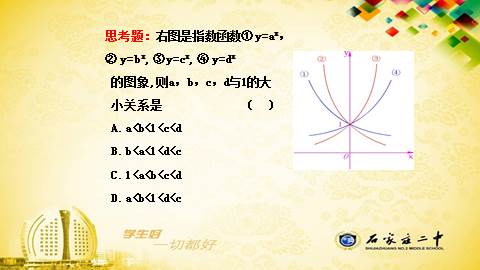
思考题：右图是指数函数① y=ax，

② y=bx, ③y=cx, ④ y=dx

的图象,则a，b，c，d与1的大

小关系是 ( )

A.a<b<1<c<d

B.b<a<1<d<c

C.1<a<b<c<d

D.a<b<1<d<c

例题讲解

例1：已知指数函数f(x)=ax(a>0且a≠1)的

图象经过点（2，16），求f(0),f(2)的值。

解：∵ f(x)的图象过点（2，16），

∴ f(2)=16即a2=16,

又a>0且a≠1

∴ a=4 ,f(x)=4x.

∴ f(0)=40=1,f(2)=42=8

即:

解:

例2. 比较下列各题中两个值的大小：

（1）1.72.5 ， 1.73

（2）0.8－0.1 ，0.8 －0.2

（3）1.70.3 ， 0.93.1.

三、图像与性质

（1）1.72.5 ， 1.73 ；

考查函数 y=

因为1.7>1，所以函数y=

<

解① ：利用函数单调性

在R上是增函数，而2.5<3，

所以，

数缺形时少直观

②

，

解② ：利用函数单调性

考查函数 y=

因为0<0.8<1，所以函数y=

在R是减函数，

而-0.1>-0.2，

<

所以，

③

，

解③ ：根据指数函数的性质，得

>

从而有

小结 ：比较指数幂大小的方法：

①、单调性法：利用函数的单调性，数的特征

是底同指不同（包括可以化为同底的）。

②、中间值法：找一个 “中间值”如“1”来过 渡, 数的特征是底不同指不同。

三、图像与性质

变式. 比较大小：

（1）3.10.5 ， 3.12.3

（2）

（3） 2.3－2.5 ， 0.2 －0.1

<

<

>

三、图像与性质

课堂小结

1、指数函数概念：

2、指数函数的图像与性质；

函数y = ax(a?0，且a ?1)叫做指数函数，其中x是自变量 .函数的定义域是R .

◆方法指导:

利用函数图像研究函数性质是一种直观而形象的方法，记忆指数函数性质时可以联想它的图像。

数形结合思想[全文已结束，注意以上仅为全文的文字预览，不包含图片和表格以及排版]

以上为《指数函数》的无排版文字预览，完整格式请下载

下载前请仔细阅读上面文字预览以及下方图片预览。图片预览是什么样的，下载的文档就是什么样的。