函数的单调性与导数

以下为《函数的单调性与导数》的无排版文字预览，完整格式请下载

下载前请仔细阅读文字预览以及下方图片预览。图片预览是什么样的，下载的文档就是什么样的。

第1章 导数及应用

1.3.1 函数的单调性与导数

复习引入：

一般地，对于给定区间D上的函数f(x)，若对于属于

区间D的任意两个自变量的值x1，x2，当x1<x2时，有

问题1：函数单调性的定义怎样描述的?

　 (1)若f(x1)<f (x2) ，那么f(x)在这个区间上是增函数.

(2)若f(x1)>f(x2)，那么f(x)在这个区间上是减函数.

(2)作差f(x1)－f(x2) (作商)

2．用定义证明函数的单调性的一般步骤：

(1)任取x1、x2∈D，且x1< x2.

(4)定号(判断差f(x1)－f(x2)的正负)(与０比较)

(3)变形(因式分解、配方、通分、提取公因式)

(5)结论

3.研究函数的单调区间你有哪些方法?

（1）观察法:观察图象的变化趋势;

（2）定义法:

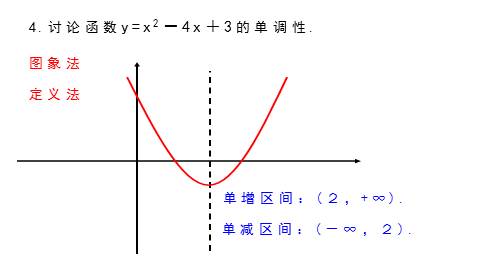
4.讨论函数y=x2－4x＋3的单调性.

定义法

单某某区间：(２，+∞).

单某某区间：(－∞，２).

图象法

5.确定函数f(x)=xlnx在哪个区间内是增函数?哪个区间内是减函数?

提出问题:(1)你能画出函数的图象吗?

(2)能用单调性的定义吗?

试一试,提问一个学生:解决了吗?到哪一步解决不了?（产生认知冲突）

发现问题:定义是解决单调性最根本的工具,但有时很麻烦,甚至解决不了.尤其是在不知道函数的图象的时候,如该例,这就需要我们寻求一个新的方法来解决．

引导：随着时间的变化,运动员离水面的高度的变化有什么趋势?是逐渐增大还是逐步减小?

函数的单调性可简单的认为是：

说明函数的变化率可以反映函数的单调性，

即函数的导数与函数的单调性有着密切的联系.

上述情况是否具有一般性呢?导数的几何意义是函数在该点处的切线的斜率,函数图象上每个点处的切线的斜率都是变化的,那么函数的单调性与导数有什么关系呢?

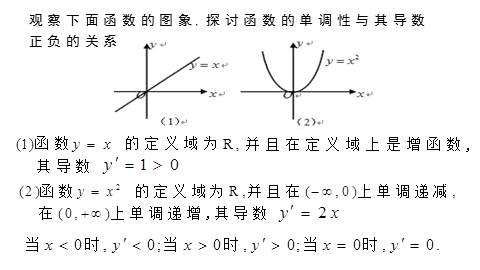
观察下面函数的图象,探讨函数的单调性与其导数正负的关系

2

.

.

.

.

.

.

.

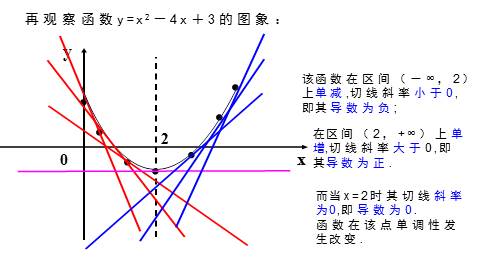
再观察函数y=x2－4x＋3的图象：

该函数在区间（－∞，2）上单某某,切线斜率小于0,

即其导数为负;

而当x=2时其切线斜率为0,即导数为0.

函数在该点单调性发生改变.

在区间（2，+∞）上单某某,切线斜率大于0,即其导数为正.

如果 ,

那么函数 在这个区间内单调递增;

如果 ,

那么函数 在这个区间内单调递减.

如果在某个区间内恒有fXXXXX(x)=0,则f(x)为常数函数.

结论：在某个区间(a,b)内,

函数在某个点处的导数值与函数在该点处的单调性的关系是：

一般地,设函数y=f(x)在某个区间(a,b)内可导,

则函数在该区间

如果在某个区间内恒有fXXXXX(x)=0,则f(x)为常数函数.

如果fXXXXX(x)<0,

则f(x)在这个区间为增函数;

则f(x)在这个区间为减函数.

如果fXXXXX(x)>0,

函数的单调性与导数的关系:

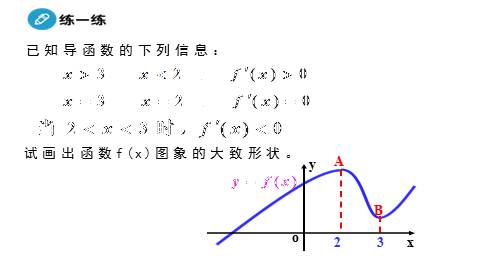
例1、已知导函数的下列信息：

试画出函数f(x)图象的大致形状。

利用导函数判断原函数大致图象

解:大体图象为

已知导函数的下列信息：

试画出函数f(x)图象的大致形状。

利用导数求函数的单调区间

例2.判断下列函数的单调性,并求出单调区间．

根据导数确定函数的单调性步骤：

1.确定函数f(x)的定义域.

2.求出函数的导数fXXXXX(x)

3.解不等式fXXXXX(x)>0,得函数单某某区间;

解不等式fXXXXX(x)<0,得函数单某某区间.

例3 如图, 水以常某某(即单位时间内注入水的体积相同)注入下面四种底面积相同的容器中, 请分别找出与各容器对应的水的高度h与时间t的函数关系图象.

(A)

(B)

(C)

(D)

h

t

O

h

t

O

h

t

O

h

t

O

从导数的角度解释增减及增减快慢的情况

解: (1)→(B),(2) →(A),(3)→(D),(4) →(C)

一般地, 如果一个函数在某一范围内导数的绝对值较大, 那么函数在这个范围内变化得快, 这时, 函数的图象就比较“陡峭”(向上或向下); 反之, 函数的图象就“平缓”一些.

有关含参数的函数单调性问题

(1)函数的单调性与导数的关系;

如何从导数的角度解释增减及增减快慢的情况;

数学知识：

(2)求解函数y=f(x)单调区间的步骤:

①确定函数y=f(x)的定义域（养成研究函数的性质从定义域出发的习惯）;

②求导数fXXXXX(x);

③得结论: fXXXXX(x)>且在定义域内的为增区间; fXXXXX(x)<0且在定义域内的为减区间．

数学思想：数形结合和转化思想．

(3)由函数在(a,b)上的单调性,求参数的取值范围:

若f(x)在区间(a,b)上是增函数,

则转化为fXXXXX(x)≥0在(a,b)上恒成立;

若f(x)在区间(a,b)上是减函数,

则转化为fXXXXX(x)≤0在(a,b)上恒成立.

然后检验参数的取值能否使fXXXXX(x)恒等于0.

必做题

1.求下列函数的单调区间：

选做题

[全文已结束，注意以上仅为全文的文字预览，不包含图片和表格以及排版]

以上为《函数的单调性与导数》的无排版文字预览，完整格式请下载

下载前请仔细阅读上面文字预览以及下方图片预览。图片预览是什么样的，下载的文档就是什么样的。