14.1.1 同底数幂的乘法
以下为《14.1.1 同底数幂的乘法》的无排版文字预览,完整格式请下载
下载前请仔细阅读文字预览以及下方图片预览。图片预览是什么样的,下载的文档就是什么样的。
14.1 整式的乘法
14.1.1 同底数幂的乘法
耿某某中学陈云
教学目标
1.理解同底数幂的乘法法则.
2.运用同底数幂的乘法法则解决一些实际问题.
重点难点
重点
正确理解同底数幂的乘法法则.
难点
正确理解和应用同底数幂的乘法法则.
教学设计
一、提出问题,创设情境
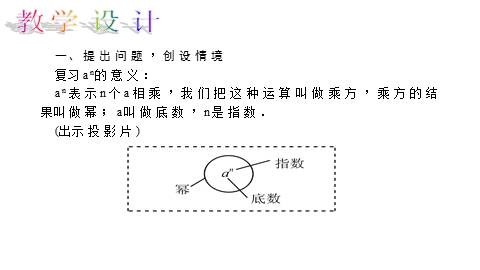
复习an的意义:
an表示n个a相乘,我们把这种运算叫做乘方,乘方的结果叫做幂;a叫做底数,n是指数.
(出示投影片)
教学设计
提出问题:
(出示投影片)
问题:一种电子计算机每秒可进行1千万亿(1015)次运算,它工作103秒可进行多少次运算?
[师]能否用我们学过的知识来解决这个问题呢?
[生]运算次数=运算速度XXXXX工作时间,
所以计算机工作103秒可进行的运算次数为:1015XXXXX103.
[师]1015XXXXX103如何计算呢?
[生]根据乘方的意义可知
1015XXXXX103=(10XXXXX10XXXXXXXXXXXXXXX10)15个10XXXXX(10XXXXX10XXXXX10)=(10XXXXX10XXXXXXXXXXXXXXX10)18个10=1018.
教学设计
提出问题:
(出示投影片)
问题:一种电子计算机每秒可进行1千万亿(1015)次运算,它工作103秒可进行多少次运算?
[师]能否用我们学过的知识来解决这个问题呢?
[生]运算次数=运算速度XXXXX工作时间,
所以计算机工作103秒可进行的运算次数为:1015XXXXX103.
[师]1015XXXXX103如何计算呢?
[生]根据乘方的意义可知
1015XXXXX103=(10XXXXX10XXXXXXXXXXXXXXX10)15个10XXXXX(10XXXXX10XXXXX10)=(10XXXXX10XXXXXXXXXXXXXXX10)18个10=1018.
教学设计
你发现了什么?注意观察计算前后底数和指数的关系,并能用自己的语言描述.
[师]根据乘方的意义,同学们可以独立解决上述问题.
[生](1)25XXXXX22=(2XXXXX2XXXXX2XXXXX2XXXXX2)XXXXX(2XXXXX2)
=27=25+2.
因为25表示5个2相乘,22表示2个2相乘,根据乘方的意义,同样道理可得
a3XXXXXa2=(aXXXXXaXXXXXa)(aXXXXXa)=a5=a3+2.
5mXXXXX5n=(5XXXXX5XXXXXXXXXXXXXXX5),\s\do4(m个5))XXXXX(5XXXXX5XXXXXXXXXXXXXXX5),\s\do4(n个5))=5m+n.
[生]我们可以发现下列规律:amXXXXXan等于什么(m,n都是正整数)?为什么?
(1)这三个式子都是底数相同的幂相乘;
(2)相乘结果的底数与原来底数相同,指数是原来两个幂的指数的和.
2.议一议
(出示投影片)
[师生共析]
amXXXXXan表示同底数幂的乘法.根据幂的意义可得:
amXXXXXan=(aXXXXXaXXXXXXXXXXXXXXXa)m个aXXXXX(aXXXXXaXXXXXXXXXXXXXXXa)n个a=aXXXXXaXXXXXXXXXXXXXXXa(m+n)个a=am+n
教学设计
教学设计
于某某amXXXXXan=am+n(m,n都是正整数),用语言来描述此法则即为:
“同底数幂相乘,底数不变,指数相加”.
[师]请同学们用自己的语言解释“同底数幂相乘,底数不变,指数相加”的道理,深刻理解同底数幂的乘法法则.
[生]am表示m个a相乘,an表示n个a相乘,amXXXXXan表示m个a相乘再乘以n个a相乘,也就是说有(m+n)个a相乘,根据乘方的意义可得amXXXXXan=am+n.
[师]也就是说同底数幂相乘,底数不变,指数要降一级运算,变为相加.
3.例题讲解
出示投影片
[例1]计算:
(1)x2XXXXXx5; (2)aXXXXXa6;
(3)2XXXXX24XXXXX23; (4)xmXXXXXx3m+1.
[例2]计算amXXXXXanXXXXXap后,能找到什么规律?
[师]我们先来看例1,是不是可以用同底数幂的乘法法则呢?
[生1](1),(2),(4)可以直接用“ 同底数幂相乘,底数不变,指数相加”的法则.
[生2](3)也可以,先算两个同底数幂相乘,将其结果再与第三个幂相乘,仍是同底数幂相乘,再用法则运算就可以了.
教学设计
[师]同学们分析得很好.请自己做一遍.每组出一名同学板演,看谁算得又准又快.
生板演:
(1)解:x2XXXXXx5=x2+5=x7;
(2)解:aXXXXXa6=a1XXXXXa6=a1+6=a7;
(3)解:2XXXXX24XXXXX23=21+4XXXXX23=25XXXXX23=25+3=28;
(4)解:xmXXXXXx3m+1=xm+(3m+1)=x4m+1.
[师]接下来我们来看例2.受(3)的启发,能自己解决吗?与同伴交流一下解题方法.
解法一:amXXXXXanXXXXXap=(amXXXXXan)XXXXXap
=am+nXXXXXap=am+n+p;
教学设计
解法二::amXXXXXanXXXXXap=amXXXXX(anXXXXXap)=amXXXXXan+p=am+n+p;
解法三:amXXXXXanXXXXXap=(aXXXXXaXXXXXa)m个aXXXXX(aXXXXXaXXXXXa)n个aXXXXX(aXXXXXaXXXXXa)p个a=am+n+p
归纳:解法一与解法二都直接应用了运算法则,同时还运用了乘法的结合律;解法三是直接应用乘方的意义.三种解法得出了同一结果.我们需要这种开拓思维的创新精神.
[生]那我们就可以推断,不管是多少个幂相乘,只要是同底数幂相乘,就一定是底数不变,指数相加.
[师]是的,能不能用符号表示出来呢?
[生]am1XXXXXam2XXXXXam3XXXXXXXXXXamn=am1+m2+m3+XXXXXmn.
[师]鼓励学生.那么例1中的第(3)题我们就可以直接应用法则运算了.
2XXXXX24XXXXX23=21+4+3=28.
教学设计
三、随堂练习
1.m14可以写成( )
A.m7+m7 B.m7XXXXXm7
C.m2XXXXXm7 D.mXXXXXm14
2.若xm=2,xn=5,则xm+n的值为( )
A.7 B.10 C.25 D.52
3.计算:-22XXXXX(-2)2=________;
(-x)(-x2)(-x3)(-x4)=________.
4.计算:(1)(-3)2XXXXX(-3)5;
(2)106XXXXX105XXXXX10;
(3)x2XXXXX(-x)5;
(4)(a+b)2XXXXX(a+b)6.
教学设计
四、课堂小结
[师]这节课我们学习了同底数幂的乘法的运算性质,请同学们谈一下有何新的收获和体会呢?
[生]在探索同底数幂乘法的性质时,进一步体会了幂的意义,了解了同底数幂乘法的运算性质.
[生]同底数幂的乘法的运算性质是底数不变,指数相加.应用这个性质时,我觉得应注意两点:一是必须是同底数幂的乘法才能运用这个性质;二是运用这个性质计算时一定是底数不变,指数相加,即amXXXXXan=am+n(m,n是正整数).
五、课后作业
教材第96页练习.
教学设计
本课的主要教学任务是“同底数幂乘法的运算性质”:同底数幂相乘,底数不变,指数相加. 在课堂教学时,通过幂的意义引导学生得出这一性质,接着再引导学生深入探讨同底数幂运算,幂的底数可以是“任意有理数、单项式、多项式”,训练学生的整体思想.
教学反思[全文已结束,注意以上仅为全文的文字预览,不包含图片和表格以及排版]
以上为《14.1.1 同底数幂的乘法》的无排版文字预览,完整格式请下载
下载前请仔细阅读上面文字预览以及下方图片预览。图片预览是什么样的,下载的文档就是什么样的。
图片预览