2.2.2反证法

以下为《2.2.2反证法》的无排版文字预览，完整格式请下载

下载前请仔细阅读文字预览以及下方图片预览。图片预览是什么样的，下载的文档就是什么样的。

2.2 直接证明与间接证明复习1.直接证明的两种基本证法：综合法和分析法2.这两种基本证法的推证过程和特点：由因导果执果索因3、在实际解题时，两种方法如何运用？通常用分析法寻求思路，再由综合法书写过程综合法已知条件结论分析法结论 已知条件 （1）如果有5只鸽子飞进两只鸽笼，至少有3只 鸽子在同一只鸽笼，对吗？（2）A、B、C三个人，A说B撒谎，B说C撒谎，C 说A、B都撒谎。则C在撒谎吗？为什么？分析:假设C没有撒谎, 则A、B都撒谎. 由A撒谎, 知B没有撒谎. 那么假设C没有撒谎不成立,则C必定是在撒谎.这与B撒谎矛盾.思考？ 把这种不是直接从原命题的条件逐步推得命题成立的证明方法称为间接证明注：反证法是最常见的间接证法，

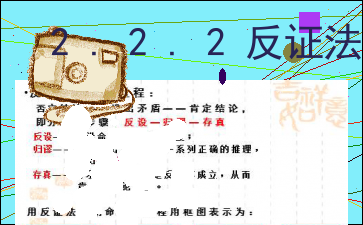
一般地，假设原命题不成立（即在原命题的条件下，结论不成立）， 经过正确的推理，最后得出矛盾。因此说明假设错误，从而证明了原命题成立， 这样的证明方法叫做反证法。理论反证法的证明过程：否定结论——推出矛盾——肯定结论，

即分三个步骤：反设—归谬—存真反设——假设命题的结论不成立；存真——由矛盾结果，断定反设不成立，从而

肯定原结论成立。归谬——从假设出发，经过一系列正确的推理， ````````得出矛盾；用反证法证明命题的过程用框图表示为： 肯定条件

否定结论导 致

逻辑矛盾反设

不成立结论

成立例1：用反证法证明：a>b>0，那么

注：直接证明难以下手的命题，改变其思维方向，从反面进行思考，问题可能解决得十分干脆。例2：

不可能成等差数列注：否定型命题(命题的结论是“不可能……”，

“不能表示为……”，“不是……”，“不存在……” ，“不等于……”，“不具有某种性质”等) 常用反证法解题反思：

证明本题时，你是怎么想到反证法的？反证法中归谬是核心步骤，本题中得到的逻辑矛盾是什么？练习：例3 已知a≠0，证明x的方程ax=b有且只有一个根。证：由于a ≠0，因此方程至少有一个根x=b/a，注:结论中的有且只有(有且仅有)形式出现,

是唯一性问题,常用反证法 ```如果方程不只一个根，不妨设x1,x2 （x1 ≠x2 )是方程的两个根.例4：已知x>0,y>0，x+y>2，

求证： 中至少有一个小于2。分 内容过长，仅展示头部和尾部部分文字预览，全文请查看图片预览。 我来这里是要被绞死。

这时，卫兵慌了神，如果他们不把这人绞死，他就说错了，就得受绞刑。可是，如果他们绞死他，他就说对了，就不应该绞死他。

为了做出决断，旅游者被送到国王那里。苦苦想了好久，国王才说——

国王：不管我做出什么决定，都肯定要破坏这条法律。我们还是宽大为怀算了，让这个人自由吧。趣味数学推理与证明推理证明合情推理演绎推理直接证明间接证明类比推理归纳推理 分析法 综合法 反证法知识结构[文章尾部最后300字内容到此结束,中间部分内容请查看底下的图片预览]

以上为《2.2.2反证法》的无排版文字预览，完整格式请下载

下载前请仔细阅读上面文字预览以及下方图片预览。图片预览是什么样的，下载的文档就是什么样的。