李某某课件

以下为《李某某课件》的无排版文字预览，完整格式请下载

下载前请仔细阅读文字预览以及下方图片预览。图片预览是什么样的，下载的文档就是什么样的。

函数

2.1.1 椭圆及其标准方程

***学 李某某

生活中的椭圆

生活中的椭圆

一、教学目标

1、知识与技能：

掌握椭圆的定义及其标准方程.

2、过程与方法：

经历公式的推导过程，体会数形结合、化归等数学思想，掌握解析法研究几何问题的一般方法。

3、情感、态度和价值观：

通过课堂活动参与，获得成功的体验，激发学生学习数学的兴趣，提高学生审美情趣，培养学生勇于探索，敢于创新的科学的精神。

二、教学重点、难点

重点：椭圆的定义及其标准方程

难点：椭圆标准方程的推导

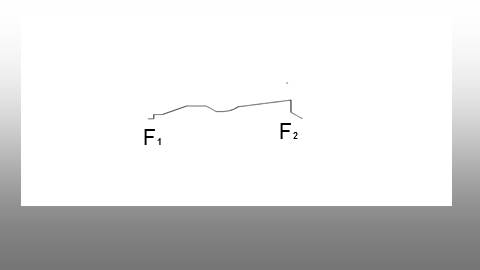
学生实验

(1)取一条细绳

(2)把它的两端固定在板上的两个定点F1、F2

(3)用铅笔尖（M）把细绳拉紧，在板上慢慢移动看看画出的 图形

【问题3】 ：在画椭圆过程中，哪些量没有变？哪些量发生了变化？

F1

F2

讨论归纳定义：

平面内，到两个定点F1、F2 的距离之和等于常数2a （2a>|F1F2|）的点的轨迹叫做椭圆。

这两个定点叫做椭圆的焦点，

两焦点的距离|F1F2|叫做椭圆的焦距。记|F1F2| =2c

M

0

【问题】：为什么2a>2c?

小组讨论，抽取一组来回答

当2a=2c时，轨迹是什么？

当2a<2c时，轨迹是什么？

三、师生互动，探索新知

【问题1 】求曲线方程的一般方法是什么？

（建系、设点、列式、化简）

【问题2】类比利用圆的对称性建立圆的方程的过程,如何利用椭圆的几何特征建立椭圆的标准方程？

方案：以F1、F2所在的直线为x轴，F1F2的中点为原点建立直角坐标系

由椭圆定义知：

【问题3】如何化简方程 ？

方法:通过两次平方化简(教科书上的做法).

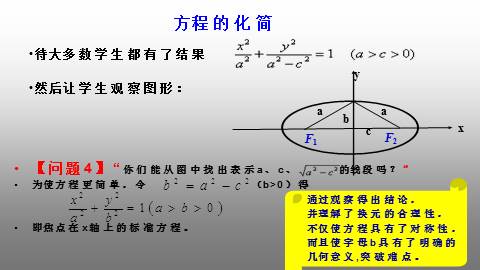
方程的化简

待大多数学生都有了结果

然后让学生观察图形：

(3)

【问题4】“你们能从图中找出表示a、c、 的线段吗？”

为使方程更简单，令 （b>0）得

即焦点在x轴上的标准方程。

通过观察得出结论，

并理解了换元的合理性，

不仅使方程具有了对称性，

而且使字母b具有了明确的

几何意义,突破难点。

c

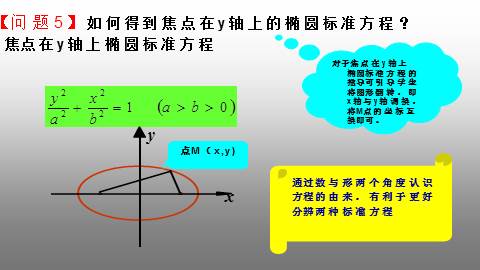
焦点在y轴上椭圆标准方程

【问题5】如何得到焦点在y轴上的椭圆标准方程？

对于焦点在y轴上椭圆标准方程的推导可引导学生将图形翻转，即x轴与y轴调换，将M点的坐标互换即可。

y

x

点M（x,y)

通过数与形两个角度认识

方程的由来，有利于更好

分辨两种标准方程

两类标准方程的对照表

定 义

图 形

方 程

焦 点

MF1+MF2=2a (2a>2c>0)

F(XXXXXc，0)

F(0，XXXXXc)

a,b,c关系

c2=a2-b2

例1：判断下列各椭圆的焦点位置，并说出焦点坐标、焦距。

（1） （2）

(3) (4)

例2：求适合下列条件的椭圆标准方程

（1）两个焦点的坐标分别为(-4,0),(4,0)，椭圆上一点P到两焦点距离的和等于10.

（2）两个焦点的坐标分别为(0,-2),(0,2)，并且椭圆经过点 (-1.5,2.5).（两种方法）

例题讲解

四、拓展升华，巩固新知

变式练习

（１）已知F1、F2是椭圆 的两个焦点，过F1的直线交椭圆于M、N两点，则 的周长为 。

（２）若方程 表示焦点在y 轴上的椭圆，则m 的取值范围是 。

通过变式练习，使学生进一步巩固知识，运用知识。

1.知识：一个定义（椭圆的定义），两类方程（焦点分别在x轴、y轴的上的两个标准方程）

2.方法：定义法和待定系数法

3.思想：数形结合、类比、分类讨论思想

五、

归纳小结

归纳小结，突出重点，构建知识网络

作业布置:

作业：1．必做题：教材P36 1，2

2．选做题:求与圆（x-2)2+y2=1外切，且与圆（x+2)2+y2=49内切的动圆圆心的轨迹方程。

体现分层教学的思想，提高学生的学习积极性，

进一步促进教学目标的实现。

[全文已结束，注意以上仅为全文的文字预览，不包含图片和表格以及排版]

以上为《李某某课件》的无排版文字预览，完整格式请下载

下载前请仔细阅读上面文字预览以及下方图片预览。图片预览是什么样的，下载的文档就是什么样的。