一元二次方某某复习
以下为《一元二次方某某复习》的无排版文字预览,完整格式请下载
下载前请仔细阅读文字预览以及下方图片预览。图片预览是什么样的,下载的文档就是什么样的。
一元二次方某某的复习
瓦亭初中数学组
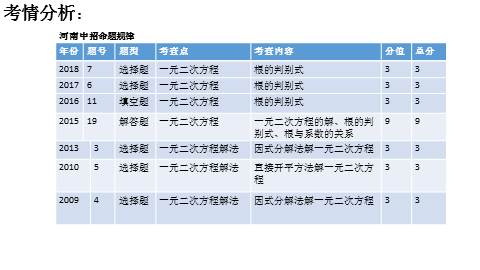
河南中招命题规律
考情分析:
★ ★ ★1、理解一元二次方某某的定义,并能将其化为一般形式;
★★★★2、会熟练解数字系数的一元二次方某某;
★ ★ ★3、能不解方某某判断一元二次方某某根的情况;
★ 4、理解一元二次方某某根与系数的关系。
复 习 目 标:
考点梳理
1.下列方某某是关于x的一元二次方某某的是( )
A.x2+2y+1=0 B. C.ax2+bx+c=0 D.3(x+)2=2(x+1)
3.已知关于X的一元二次方某某(m-2)x2+mx+m2-4=0的一根为零,则m的值为 ( )
A.XXXXX2 B.-2 C.2 D.0
对点训练一:
2.一元二次方某某3X2-X=2化为一般形式为 二次项系数为 ;一次项 是 常数项是 .
考点总结 一元二次方某某的定义
1.只含有 一 个未知数,并且未知数的最高次数是 2 ,这样的整式方某某叫做一元二次方某某,一元二次方某某的一般形式是 ax2+bx+c=0(a,b,c是常数,且a≠0) .
2.一元二次方某某的解:使一元二次方某某两边相等的未知数的值叫做一元二次方某某的解,也叫做一元二次方某某的根.
D
3X2-X-2 =0
3
-X
-2
B
温馨提醒:若有困难不要忘记课本是你最好的老师。
1.(2009河南)方某某X2=X的解是( )
A.X=1 B.X=0 C.X1=1,X2=0 D.X1=-1,X2=0
2.(2016新疆)一元二次方某某x2-6x-5=0配方可变形为( )
A.(x-3)2=14 B.(x-3)2=4 C.(x+3)2=14 D.(x+3)2=4
对点训练二:
3.(2010桂林)一元二次方某某x2+3x-4=0的解是( )
A.x1=1,x2=-4 B.x1=-1,x2=4 C.x1=-1,x2=-4 D.x1=1,x2=4
C
A
A
㩳
≠
㩳
注意:只有一元二次方某某有根的判别式,在逆用判别式时一定要保证二次项系数不等于零.
1.(枣庄2016)下列一元二次方某某中,没有实数根的是( )
A.x2 -2x-3=0 B x2 -x+1=0 C.x2+2x+1=0 D.x2=1
2.(2016河南)若关于x的一元二次方某某x2+3x-k=0有两个不相等的实数根,则k的取值范
围是
对点训练三:
考点三 一元二次方某某根的判别式b2-4ac.(课本第 32 页)
1.b2-4ac>0?一元二次方某某ax2+bx+c=0(a≠0)有两个不相等的实数根
2.b2-4ac=0?一元二次方某某ax2+bx+c=0(a≠0)有两个相等的实数根,
3.b2-4ac<0?一元二次方某某ax2+bx+c=0(a≠0)没有实数根;
B
变式训练:若关于x的一元二次方某某kx2 +3x-1=0有两个不相等的实数根,则k的取值范
围是
对点训练四:
1.已知方某某x2+3x-5=0的两个根分别为x1、x2,则x1+x2-x1?x2的值 ;
3.(2016雅安)已知关于x的一元二次方某某x2+mx-20=0的一个实数根为-4,则另一实数根及m的值分别为
( )
A.5,-1 B.-5,-1 C.5,1 D.-5,1
2.方某某2x 2- 3x- 5=0的两根之和是 ,两根之积是 ;
考点四 一元二次方某某根与系数的关系
关于x的一元二次方某某ax2+bx+c=0(a≠0)有两根分别为x1、x2,则
x1+x2= x1?x2=
注意:在应用根与系数的关系时,一定要保证一元二次方某某有实数根。
2
A
重点再练
一、用适当的方法解下列方某某:
1、2x2 =6
2、4(1 -x ) 2 - 9 =0
3、x2 + 2x = 5
4、2x2 +x - 6 = 0
二、已知:关于x的方某某x2 - (2k + 1) x+k2 = 2
(1)、当k取何值时,该方某某有两个不相等的实数根?
(2)、 当k取何值时,该方某某有两个相等的实数根?
(3) 、当k取何值时,该方某某没有实数根?
(4) 、当k取何值时,该方某某有两个实数根?
方法总结:
解一元二次方某某时,要注意根据方某某的特点,选择适当的方法求解。一般地,当方某某缺少一次项或者左边是一个完全平方式,右边是一个非负数或完全平方式,宜采用直接开平方法;若缺少常数项或者一边为0,另一边易于分解因式宜用因式分解法;若二次项系数化为1,且一次项系数是偶数时,宜用配方法。否则,就用公式法。
(2015河南)已知关于x的一元二次方某某(x-3)(x-2)=?m?.
(1)求证:对于任意实数m,方某某总有两个不相等的实数根;
(2)若方某某的一根是1,求m的值及方某某的另一根.
直击中考
1.方某某 x(x+3)=(x+3)的根为( )
A.x1=1,x2=3 B.x1=1,x2=-3 C.x=1 D.x=-3
2.(2010?荆门)如果方某某ax2+2x+1=0有两个不等的实数根,则实数a的取值范围是( )
A.a<1 B.a<1且a≠0 C.a≤1 D.a≤1且a≠0
变式一:如果方某某ax2+2x+1=0有两个的实数根,则实数a的取值范围是
变式二:如果方某某ax2+2x+1=0有实数根,则实数a的取值范围是
3.设x1、x2 是方某某x2+ 3x-3 =0的两个实数根,则 的值为( )
A.5 B.-5 C.1 D.-1
4.已知m、n是方某某x2 +2x-5=0的两个实数根,则m2-mn+3m+n=
5.若关于x的一元二次方某某的两个实数根为1和2,则这个方某某为( )
A.x2 +3x-2=0 B.x2 -3x+2=0 C.x2 -2x+3=0 D.x2 +3x+ 2=0
6.(2010?中山)已知一元二次方某某x2-2x+m=0.
(1)若方某某有两个实数根,求m的范围;
(2)若方某某的两个实数根为x1、x2,且x1+3x2=3,求m的值.
课堂检测
课堂小结
你熟悉了哪些知识和方法?
你有解一元二次方某某的秘诀吗?
分享话吧
作业设计
必做题:
九年级上册课本P36页
第4题(2)、(3)、(5)、(6)、(7)、(8)
第7题、第8题、第11题
选做题:
已知关于x的一元二次方某某x2-6x+(2m+1)=0有实数根.
(1)求m的取值范围.
(2)如果方某某的两个实数根为x1,x2,且2x1x2+x1+ x2≥20,求m的取值范围.
谢 谢 指 导!
再 见[全文已结束,注意以上仅为全文的文字预览,不包含图片和表格以及排版]
以上为《一元二次方某某复习》的无排版文字预览,完整格式请下载
下载前请仔细阅读上面文字预览以及下方图片预览。图片预览是什么样的,下载的文档就是什么样的。
图片预览