椭圆第一定义
以下为《椭圆第一定义》的无排版文字预览,完整格式请下载
下载前请仔细阅读文字预览以及下方图片预览。图片预览是什么样的,下载的文档就是什么样的。
2.1.1椭圆的定义
与标准方程
每当我们w箍铡?
当我们看到这种形状的建筑XXXXXXXXXX.
以及这些日用品XXXXXXXXXX
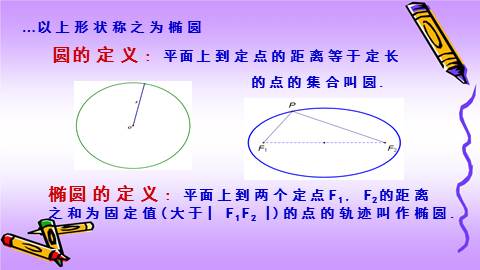
XXXXX以上形状称之为椭圆
圆的定义: 平面上到定点的距离等于定长
的点的集合叫圆.
椭圆的定义: 平面上到两个定点F1, F2的距离之和为固定值(大于| F1F2 |)的点的轨迹叫作椭圆.
2.改变两图钉之间的距离,使其与绳长相等,画出的图形还是椭圆吗?
3.绳长能小于两图钉之间的距离吗?
实验环节:
1.找3位同学,拿出一段绳子,画出椭圆。
圆标准方程推导步骤
?提出问题→解决问题.
如何推导椭圆的标准方程呢?
? 求动点轨迹方程的一般步骤:
1、建立适当的坐标系,用P(x,y)表示曲线上任意一点(动点)的坐标;
2、写出适合条件 的等量关系 ;
3、用坐标表示条件P(M),列出方程 ;
4、化方程为最简形式。
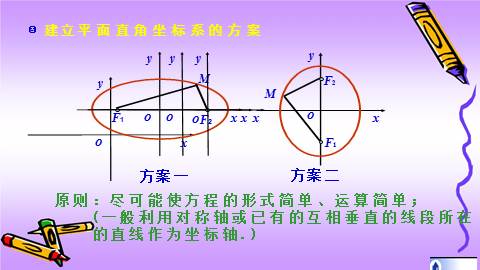
? 建立平面直角坐标系的方案
方案一
原则:尽可能使方程的形式简单、运算简单;
(一般利用对称轴或已有的互相垂直的线段所在
的直线作为坐标轴.)
x
?设P (x, y)是椭圆上任意一点,
椭圆的焦距|F1F2|=2c(c>0),
则F1、F2的坐标分别是(?c,0)、(c,0) .
P与F1和F2的距离的和为固定值2a(2a>2c)
(问题:下面怎样化简?)
由椭圆的定义得,限制条件:
由于
得方程
由椭圆定义可知
整理得
两边再平方,得
移项,再平方
刚才我们得到了焦点在x轴上的椭圆方程,
如何推导焦点在y轴上的椭圆的标准方程呢?
(问题:下面怎样化简?)
由椭圆的定义得,限制条件:
由于
得方程
?
Y
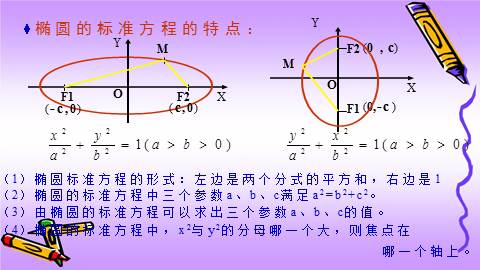
?椭圆的标准方程的特点:
(1)椭圆标准方程的形式:左边是两个分式的平方和,右边是1
(2)椭圆的标准方程中三个参数a、b、c满足a2=b2+c2。
(3)由椭圆的标准方程可以求出三个参数a、b、c的值。
(4)椭圆的标准方程中,x2与y2的分母哪一个大,则焦点在
哪一个轴上。
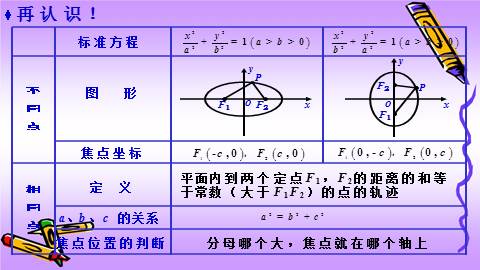
分母哪个大,焦点就在哪个轴上
平面内到两个定点F1,F2的距离的和等
于某某(大于F1F2)的点的轨迹
?再认识!
则a= ,b= ;
则a= ,b= ;
5
3
4
6
口答:
则a= ,b= ;
则a= ,b= .
3
例3.求下列椭圆的焦点坐标,以及椭圆上
每一点到两焦点距离的和。
解:椭圆方程具有形式
其中
因此
两焦点坐标为
椭圆上每一点到两焦点的距离之和为
如图:求满足下列条件的椭圆方程
解:椭圆具有标准方程
其中
因此
所求方程为
例4. 求出刚才在实验中画出的椭圆的标准方程
小结:
求椭圆标准方程的方法
求美意识, 求简意识,前瞻意识
分母哪个大,焦点就在哪个轴上
平面内到两个定点F1,F2的距离的和等
于某某(大于F1F2)的点的轨迹
再见![全文已结束,注意以上仅为全文的文字预览,不包含图片和表格以及排版]
以上为《椭圆第一定义》的无排版文字预览,完整格式请下载
下载前请仔细阅读上面文字预览以及下方图片预览。图片预览是什么样的,下载的文档就是什么样的。
图片预览