1.7.1定积分在几何中的应用

以下为《1.7.1定积分在几何中的应用》的无排版文字预览，完整格式请下载

下载前请仔细阅读文字预览以及下方图片预览。图片预览是什么样的，下载的文档就是什么样的。

主讲：刘某某

1.7.1定积分在几何中的应用

***学

旧知回顾

课堂环节

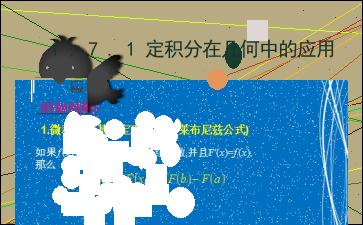
1.微积分的基本定理(牛顿－莱布尼兹公式)

旧知回顾：

如果f (x)是区间[a,b]上的连续函数,并且F?(x)=f (x),

那么

2.定积分的几何意义

(在x轴上方的面积对应积分取正号,

、

在x轴下方的面积对应积分取负号)

1.定积分的几何意义

c

d

新知探究：

①

②

③

④

⑤

2.常见曲边图形的面积

牛刀小试：用定积分表示下列阴影部分的面积.

例1 计算由曲线y2=x, y=x2 所围成图形的面积S.

典例探究：

解

两曲线的交点 (0,0),(1,1)

3．利用定积分求平面图形的面积的步骤

(1) ，在直角坐标系中画出曲线或直线的大致图象．

(2)确定积分的 ，需要求出交点的坐标．

借助图形确定出被积函数．

(3)确定 ，注意区分函数的上下位置.

(4)求 ，用微积分基本定理计算定积分，求出曲边图形的面积

上、下限

画出草图

被积函数

定积分

变式1：求曲线y＝x2与直线y＝2x所围图形的面积S.

变式2.求由y=ex, x=2, y=1围成的曲边梯形的面积.

例2：求y=x2, x=-1, x=1, y=0围成平面图形的面积.

S=S1+S2

解:

两曲线交点为(8,4)

直线y=x-4与x轴的交点为(4,0)

S=S1+S2

S=S1+S2

4

8

解:

三曲线交点为(0，0)，（1,1），（3，-1）

1：求下列曲线所围成的图形的面积

(1) y=x2, y=2x+3; (2) y=ex, y=e, x=0

反馈练习：

3.求由曲线xy＝1及直线y＝x，y＝2所围成的平面图形的面积．

解:

三曲线交点为

2.利用定积分求平面图形的面积的步骤

(1) ，在直角坐标系中画出曲线或直线的大致图象．

(2)确定积分的 ，需要求出交点的坐标．

借助图形确定出被积函数．

(3)确定 ，注意区分函数的上下位置.

(4)求 ，用微积分基本定理计算定积分，求出曲边图形的面积

上、下限

课堂小结;

画出草图

被积函数

被积函数

定积分

1.定积分的几何意义

①

②

③

④

⑤

3.常见曲边图形的面积

谢谢指导

Thank

you

for

your

guidance[全文已结束，注意以上仅为全文的文字预览，不包含图片和表格以及排版]

以上为《1.7.1定积分在几何中的应用》的无排版文字预览，完整格式请下载

下载前请仔细阅读上面文字预览以及下方图片预览。图片预览是什么样的，下载的文档就是什么样的。