直线与圆的位置关系

以下为《直线与圆的位置关系》的无排版文字预览，完整格式请下载

下载前请仔细阅读文字预览以及下方图片预览。图片预览是什么样的，下载的文档就是什么样的。

4.2 直线、圆的位置关系

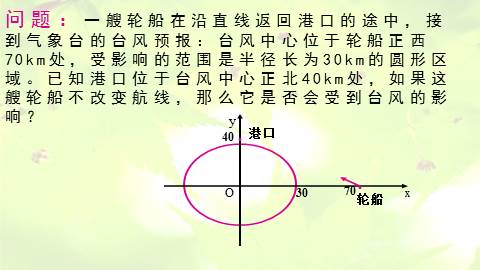
问题：一艘轮船在沿直线返回港口的途中，接到气象台的台风预报：台风中心位于轮船正西70km处，受影响的范围是半径长为30km的圆形区域。已知港口位于台风中心正北40km处，如果这艘轮船不改变航线，那么它是否会受到台风的影响？

40

70

30

4.2.1 直线与圆的位置关系

直线与圆的位置关系有几种？

(1)直线与圆相交，有两个公共点；

(2)直线与圆相切，只有一个公共点；

(3)直线与圆相离，没有公共点；

问题：如何用直线和圆的方程判断它们之间的位置关系？

(1)利用圆心到直线的距离d与半径r的大小关系判断：

直线与圆的位置关系的判定方法：

直线l：Ax+By+C=0

圆C：(x-a)2+(y-b)2=r2(r>0)

直线与圆相离

直线与圆相切

直线与圆相交

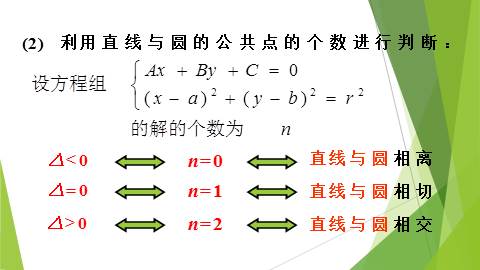
(2) 利用直线与圆的公共点的个数进行判断：

直线与圆相离

直线与圆相切

直线与圆相交

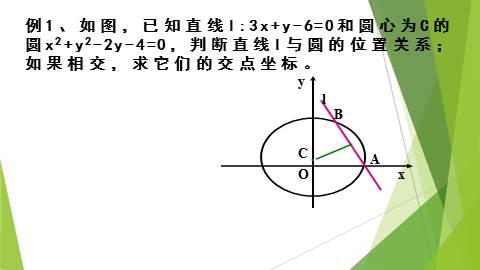
例1、如图，已知直线l:3x+y-6=0和圆心为C的圆x2+y2-2y-4=0，判断直线l与圆的位置关系；如果相交，求它们的交点坐标。

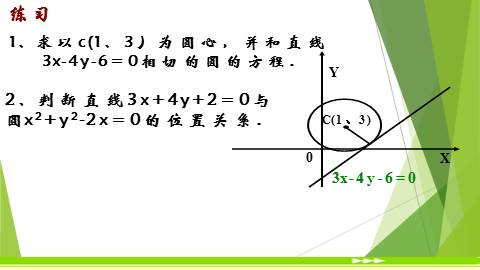
练习

1、求以c(1、3）为圆心，并和直线

3x-4y-6=0相切的圆的方程.

2、判断直线3x+4y+2=0与

圆x2+y2-2x=0的位置关系.

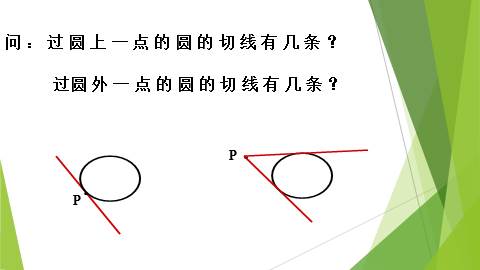
问：过圆上一点的圆的切线有几条？

过圆外一点的圆的切线有几条？

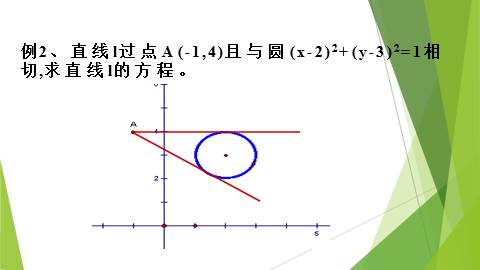
例2、直线l过点A(-1,4)且与圆(x-2)2+(y-3)2=1相 切,求直线l的方程。

例2、直线l过点A(-1,4)且与圆(x-2)2+(y-3)2=1相 切,求直线l的方程。

注意：利用斜率研究直线时，要注意直线斜率不存在的情形，应通过检验，判断它是否符合题意。

当点A的坐标为(2,2)或(1,1)时，结果有变化吗？

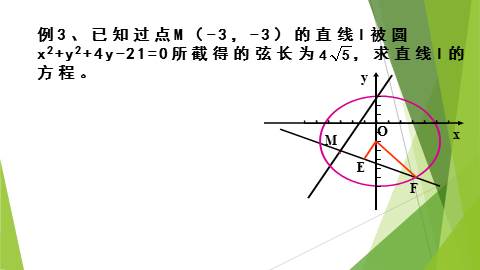
已知直线L:kx-y+6=0被圆x2+y2=25截得的弦长为8,求k值

练习：

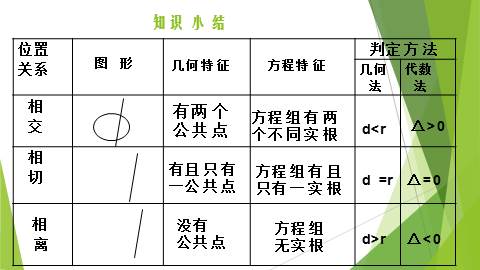
知识小结

有两个

公共点

方程组有两

个不同实根

d<r

△>0

有且只有

一公共点

方程组有且

只有一实根

d =r

△=0

没有

公共点

方程组

无实根

d>r

△<0

方法小结：

1、判定直线 与圆的位置关系的方法有两种

(1)代数方法，由直线 与圆的公共点 的个数来判断

(2)几何方法，由圆心到直线的距离d与半径r的关系判断。

在实际应用中，常采用第二种方法判定。

2、利用斜率研究直线时，要注意直线斜率不存在的

情形应通过检验，判断它是否符合题意。

1.如图,圆x2+y2=4上有___个点,到直线3x+4y-5=0 的距离为1.

研究性问题

2.对任意实数k,圆C: x2+y2-6x-8y+12=0与直线L:kx-y-4k+3=0的位置关系是( )

A 相交 B相切 C相离 D与k值有关

3.若方程组 有唯一解，求K的

取值情况。 [全文已结束，注意以上仅为全文的文字预览，不包含图片和表格以及排版]

以上为《直线与圆的位置关系》的无排版文字预览，完整格式请下载

下载前请仔细阅读上面文字预览以及下方图片预览。图片预览是什么样的，下载的文档就是什么样的。